楕円曲線のEdwards formについて
#数楽 リンクメモhttp://hyperelliptic.org/EFD/ Explicit-Formulas Database of genus-1 curves
#数楽 メモ続きhttps://cr.yp.to/talks/2009.03.26/slides.pdf …Models of Elliptic CurvesBernstein-Lange 2009 Slides
#数楽 メモ続きhttp://dergipark.gov.tr/download/article-file/147976 …On the Alternate Models of Elliptic Curves Muhammad Ashraf and Baris Buelent Kirlar 2012
#数楽 メモ続きhttps://www.cryptojedi.org/papers/edpair-20100520.pdf …Faster Computation of the Tate PairingArenea-Lange-Naehrig-Ritzenthalera楕円曲線のEdwards form
#数楽 Edwards formの話を知らなかった。暗号との関係で楕円曲線の群構造のコンピューター上での実現の仕方による計算の速さの違いが細かくかつ具体的に研究されているんですね。Edwards formでの加法定理の具体形は結構シンプル。楕円量子群の話などにも役立つかも。
#数楽 楕円曲線のEdwards formは円の2パラメータ変形のax^2+y^2=1+dx^2y^2.複素数体上ならa=1とできてx^2+y^2=1+dx^2y^2.d=0で単位円周になる。楕円曲線のこの表示の話を今日まで知らなかった。ググって知った。
#数楽 続き。興味深いのはこの座標での群構造の形で(x1,y1)+(x2,y2)=((x1y2+x2y1)/(1+dx1x2y1y2), (y1y2-ax1x2)/(1-dx1x2y1y2)).a=1,d=0なら(x,y)=(sin θ, cos θ)で円周の群構造。
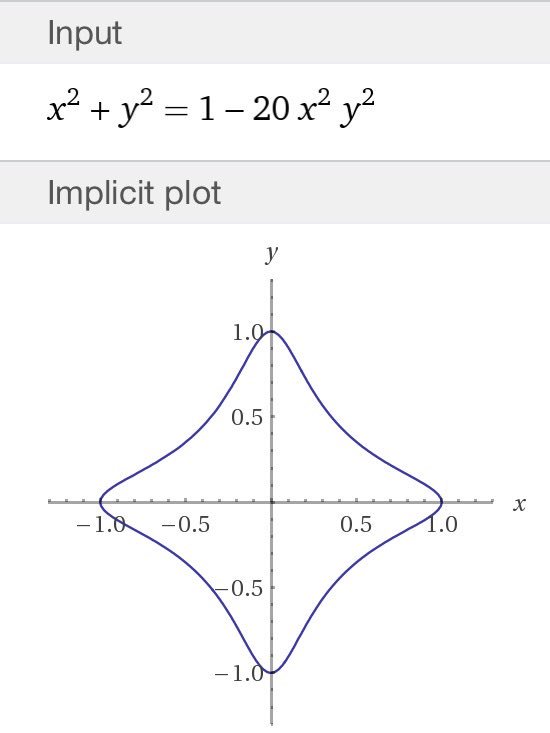
#数楽 楕円曲線のEdwards formならパラメータの特殊化で単位円周を含んでいるので上手に整備すれば「大学初年級や高校レベルでの教育」にも利用し易いかもしれないですね。誰か実際に周辺を整備してくれないものかな。楕円曲線と楕円函数のいい勉強になると思います。
#数楽 リンクメモhttp://www.ams.org/journals/bull/2007-44-03/S0273-0979-07-01153-6/S0273-0979-07-01153-6.pdf …A normal form for alliptic curvesH.M.Edwards2007楕円曲線のEdwards formの原論文。Eulerさんの論文も引用している。
#数楽 リンクメモhttps://crypto.stackexchange.com/questions/43439/elliptic-curves-in-edwards-form-or-edwards-curve-and-addition-formulas …暗号のStackExchangeにおける楕円曲線のEdwards formでの群構造の表示の証明に関する質問。
#数楽 リンクメモhttp://iml.univ-mrs.fr/ati/crypto_puces/2011/slides/Mardi/rolland.pdf …Elliptic curves - Edwards formR.RollandSlides 2011
#数楽 Rollandさんの解説ではEdwards formをWeierstrass formへの変換を具体的に行うことによってEdwards formでの加法公式を導出する方針になっていますね。原論文の方は扱っている曲線の表示が少し違うのですが、色々なことが書いてあります。
#数楽 続き。「Edwards formでの加法公式を初等的に説明してみろ」と言われると「全部自分で準備するのはちょっと面倒そうだな」と思ったので、またググってみました。というわけでリンクメモ続き。https://arxiv.org/abs/1610.05278 これ結構最近
#数楽 続き。高校で数学を教えている人が三角函数の加法定理に関する理解を深めるためにも https://arxiv.org/abs/1610.05278 は役に立ちそうです。一般にAについて「十分に理解した」という気分になれるのはAより一段上のA'について理解したときだと思う。
#数楽 https://arxiv.org/abs/1610.05278 (と基本文献 https://www.cryptojedi.org/papers/edpair-20100520.pdf … )にはx^2+y^2=1の群構造に制限しても知らない話が書いてあった。要するに三角函数の加法定理の理解が不十分だったことに気付かされました。笑!!!
#数楽 楕円曲線の暗号への応用が動機になって、楕円曲線の様々な標準形(よくある教科書に書いてあるのはWeierstrassの標準形)とその標準形における加法公式の具体形が詳細に研究されました。その過程で10年前にEulerさんやGaussさんの計算にヒントを得て〜続く
#数楽 続き~、単位円周を特殊化として含むEdwards curveを考えると、加法公式など様々な公式がシンプルになることに気付きました。これが楕円曲線のEdwards formの話です。
#数楽 レムニスケートの孤の長さと楕円函数の特殊な場合に関する話は有名なのでググればたくさんの解説が見つかります。https://www.google.co.jp/search?q=�%83�ムニスケートの孤長 …
#数楽 z^2=1-x^4の話は有名なので知ってました。z=y(1+x^2)を代入して両辺を1+x^2で割って整理するとx^2+y^2=1-x^2y^2と単位円周に近い式の曲線が得られます。これをGaussさんより前にEulerさんが扱っていたらしい。すべてがEulerに繋がる。
#数楽 Civilizationのようなゲームであるとうれしいのはエカテリーナ二世がオイラーを手に入れると科学の発展と宗教の普及が加速するというようなイベント。しかし科学アカデミーに予算を割かないとオイラーさんは出て行ってしまう。オイラーさんは色々面白い人です。
#数楽 で、EdwardsさんはEuler-Gaussの計算がx^2+y^2=a^2(1+x^2y^2)の場合に綺麗に一般化できることを見つけました。x^2+cy^2=1+dx^2y^2の場合が https://arxiv.org/abs/1610.05278 で扱われています。続く
#数楽 続き。c=1,d=0の場合が単位円周x^2+y^2=1です。そこには角度θによって加法構造が自然に入り、単位円周はAbel群になります。三角函数の加法定理は加法構造をxy座標で表示したものに一致します。角度θの助けを借りなくても、加法構造を記述できる。続く
#数楽 x^2+y^2=1の加法構造の公式(x1,y1)+(x2,y2)=(x1x2-y1y2,x1y2+y1x2)右辺はxi=cos θi, yi=sin θi とおけば三角函数の加法定理の式になっています。右辺は三角函数を知らなくても計算できる。
#数楽 この加法構造は次のように幾何的な記述を持ちます。双曲線xy+p(x+1)+qy=0とx^2+y^2=1の4つの交点を(-1,0),(xi,yi) (i=1,2,3)と書くと、(x1,y1)+(x2,y2)=(x3,-y3).私が知らなかったのはこれ。
#数楽 楕円曲線x^2+cy^2=1+dx^2y^2の加法構造もまったく同様に特徴付けられます。この方針での三角函数の加法定理の証明もできるわけですが、Edwards curvesの文献を見るまで知りませんでした。三角函数の加法定理をよく理解してなかったことがわかりました。
#数楽 まさか、ググって見つけた楕円曲線の暗号への応用関係の文献を見て、楕円函数以前に三角函数への理解の足りなさを認識することになるとは思って無かった。自分自身の無知無能には、気付く機会がないと、一生気付かないものだと思う。気付けたのはラッキーです。
#数楽 以上の話の x^2+y^2=1 関係の部分は明らかに高校レベルの話なので、興味を持った高校生は色々計算してみると良いと思います。私の説明がまずいせいでわかりにくいところは自分で計算すればクリアになると思います。どっちにしろ、自分で計算しないと数学は理解できない。

#数楽 添付図はEdwards曲線の例と(-1,0)を通りx軸とy軸に平行な漸近線を持つ双曲線が4点で交わっている図。この図でEdwards曲線の加法構造が定義される。(-1,0)以外の3交点の和は0。単位元は右端。逆元を取る操作は上下反転。pic.twitter.com/74eTpxtamZ
#数楽 楕円曲線のEdwards形でのアーベル群構造の公式をコンピューターでチェックしてみました。円の場合が丁度cosとsinの加法定理の形になることの確認は、答えがそうなることを知っていれば、そう難しくないので、いつか大学入試ネタで使われることもあるかもしれませんね。続く
#数楽 楕円曲線のEdwards formとはx^2+cy^2=1+dx^2y^2のことです。c=1,d=0とすると、x^2+y^2=1と円になる。Edwards formでの群構造は双曲線との交わりで特徴付けられます。その円の場合への特殊化は高校レベルの式になる。続く
#数楽 続き。E曲線x^2+cy^2=1+dx^2y^2上の3点(-1,0),(x1,y2),(x2,y2)を通る双曲線xy+p(x+1)+qy=0とE曲線の4つ目の交点を(x3,y3)とするとき、群構造は(x1,y1)+(x2,y2)=(x3,-y3)と定義されます。続く
#数楽 続き。高校レベルの問題:c=1,d=0の円のとき、(x1,y1)+(x2,y2)=(x1x2-y1y2,x1y2-x2y1)となることを確認せよ。実はすでに返答連鎖の中で書いたようにこの結果を私は知りませんでした。単純な計算で確認できます。(油断すると苦労する。)
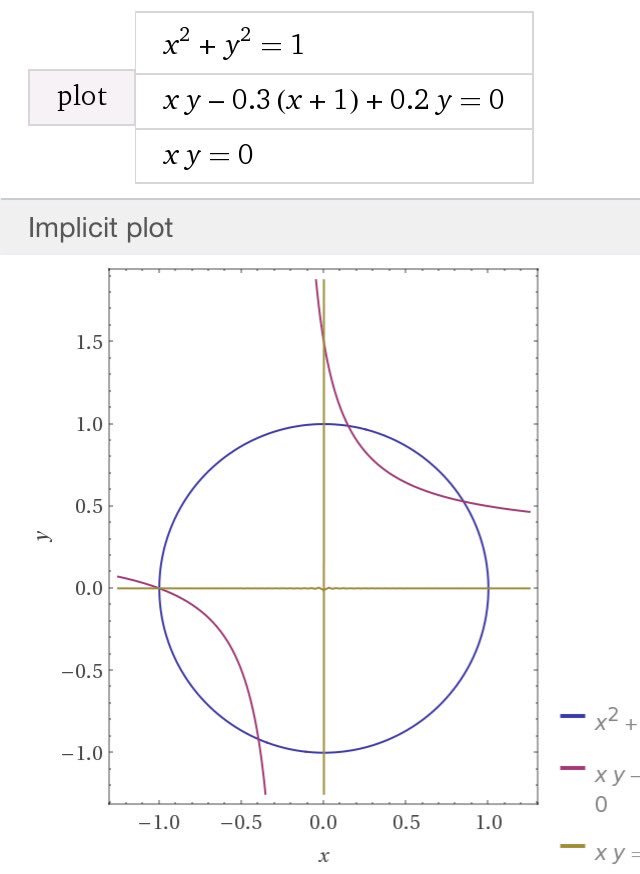
#数楽 実際に円と件の双曲線をWolframAlphaで作図してみるとこうなります。円と双曲線の(-1,0)以外の3交点の偏角の和が0になる様子が見えます。これに高校レベルの直観的な説明を付けられた人がいたら教えて下さい。http://www.wolframalpha.com/input/?i=plot%20x^2+y^2=1, xy-0.3(x+1)+0.2y=0, xy=0 …pic.twitter.com/0txPi3pEti
#数楽 円上の点の偏角の和がある種の双曲線との交点で特徴付けられることについて、高校レベルの直観的説明があるはずなのですが、私はまだ何も考えていません。関連の基本文献へのリンクはこの発言の返答連鎖の中にあります。数学の論文は最近のものならほぼ確実にインターネットで無料で読めます。
#数楽 問題訂正!いつもの符号の誤り。センスのある人なら困らない訂正可能な誤り。問題:リンク先の問題を自力で訂正して解いてみよ(笑)。https://twitter.com/genkuroki/status/855057783741218817 …
#数楽 一応訂正しておきます。高校レベルの問題訂正版:c=1,d=0の円のとき、(x1,y1)+(x2,y2)=(x1x2-y1y2,x1y2+x2y1)となることを確認せよ。xi=cos θi, yi=sin θi とおくと三角函数の加法定理の形になっています。
#数楽 この結果の確認は中学生でもがんばればできるはずです。所謂「文字式」の単純な計算でしかない。実際に確認できた中学生は、大学院レベルの方法で三角函数の加法定理の確認をしたことになり、高校と大学をいきなり飛び越えたことになります(笑)。
#数楽 計算の筋道x3=x1x2-y1y2, y3=-(x1y2+x2y1)とおきます。(x1,y1)と(x2,y2)がx^2+y^2=1をみたしていることから、(x3,y3)もx^2+y^2=1を満たすことが簡単にわかります。続く
#数楽 続き。(x1,y1)と(x2,y2)がxy+p(x+1)+qy=0の解であることからpとqをx1,y1,x2,y2で表せます。(x3,y3)をxy+p(x+1)+qyに代入してxi^2+yi^2=1を使うと0になることを確認できます(ここが一番面倒な部分)。続く
#数楽 続き。最後のステップだけがちょっと面倒なのですが、xi^2を機械的に1-yi^2で置き換えれば、分子がキャンセルして0になることを、完全に機械的な計算で確認できます。コンピュータを使えば式を入力するだけで計算が終了します。続く
#数楽 続き。私は久々にREDUCE https://sourceforge.net/projects/reduce-algebra/files/?source=navbar … を使ってみました。有理式を気軽に扱うには結構便利です。置き換えはlet x1^2=1-y1^2;と宣言しておく。代入は:=であることに注意。検索すれば使い方はすぐにわかります。
#数楽 円とは限らない一般の場合は(x1,y1)+(x2,y2)=((x1x2-cy1y2)/(1-dx1x2y1y2),(x1y2+x2y1)/(1+dx1x2y1y2))です。これもREDUCEに10行くらい入力すれば確認できます。これは実質的に楕円函数の加法公式。続く
#数楽 円とは限らない一般の場合も計算の仕方は円の場合と同じなのですが、手計算による難易度は全然違います。やろうとしてみればわかります。円の場合は手計算でも易しい。しかし原理的に同じ方法でしょうめいできるので、中学生でも確認できる人達がいるはずです。続く
#数楽 続き。以上のEdwards formでの計算には教育的に大きな利点があるように思えます。なぜならば高校生ならみんな知っている円の場合(三角函数の加法定理と同じ公式)を直接的に含んでいるからです。そして結果の式も楕円曲線の他の標準形よりシンプルです。
#数楽 続き。以上は所謂代数曲線としてのEdwards曲線の取り扱いです。リーマン面として扱ってEdwards曲線の上の楕円函数論を誰か書くと良いかもしれません。Edwards formはJacobiの楕円テータ函数とも相性が良さそうです。
#数楽 Edwards曲線の式はx^2=(1-cy^2)/(1-dy^2)と書き直せるので、明らかに楕円積分のJacobi型標準形と相性が良いです。https://ja.m.wikipedia.org/wiki/楕円積分 …
#数楽 リンク先の訂正。自明なひどい誤り。ガウスさんがレムニスケートの孤長との関係で扱った楕円曲線はもちろんz^2=1-x^4.中学数学の教科書には意味が無さそうな文字式がたくさん書いてあるが、意味のあるやつの方がうれしい。https://twitter.com/genkuroki/status/854349852624297984 …
#数楽 以上の連続ツイートの内容について、リンク先の図と説明を理解してもらえれば、私が言いたいことのちょうど半分を理解してもらえたことになります。式は後回しでいいです。計算する気がない人が式を真面目に見てもあんまり意味がないです。https://twitter.com/genkuroki/status/855060809860268033 …
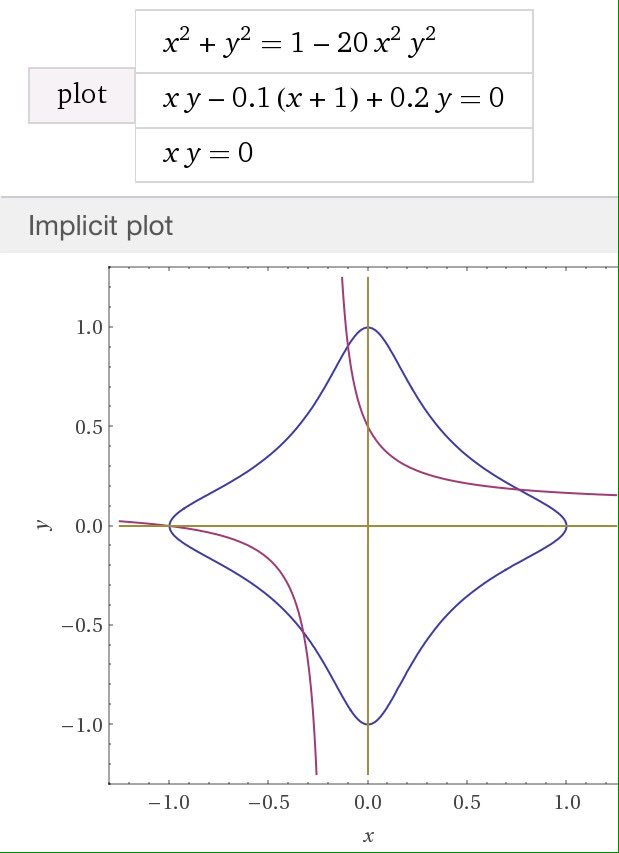
#数楽 続き。次の図が楕円曲線の群構造の特徴付けになっているという話が、私がみんなに伝えたいと思っていることの残りの半分です。円の場合の直接的一般化になっている。円の場合と楕円曲線の場合の群構造の定義の仕方が完全に同じ形!http://www.wolframalpha.com/input/?i=plot%20x^2+y^2=1-20 x^2 y^2, xy-0.1(x+1)+0.2y=0, xy=0 …pic.twitter.com/LSAK34iRkN
#数楽 以上で使った図はiPhone上のWolframAlphaの有料アプリ(安いです)で作りました。スクリーンショットを切り取った。私が子供の保護者なら、たとえうざいと言われてもそのアプリは子供の携帯に強制インストールしたいです。
#数楽 リンクメモElliptic Curve Addition Without Tearshttps://jiggerwit.wordpress.com/2016/10/18/elliptic-curve-addition-without-tears/ …GIF動画で円およびEdwards曲線の場合の双曲線との交点を使った群構造の特徴付けを観察することができる。
#数楽 リンクメモ楕円曲線のEdwards formの暗号への応用https://en.wikipedia.org/wiki/EdDSA (日本語版はなんかおかしい https://ja.wikipedia.org/wiki/エドワーズ曲線デジタル署名アルゴリズム … 「同値」の「同」の字が欠けていたりする)
#数楽 リンクメモhttp://herumi.github.io/ango/ の17.11,17.12(p.195)にEdwards曲線に関する解説がある。もちろんこれも楕円曲線暗号関係の話。
#数楽 楕円曲線のEdwards formでの加法公式は高校で習う三角函数の加法公式の直接的一般化になっているので、高校で三角函数の加法公式を教えるときに「これをちょこっと一般化した場合が我々のプライバシーを守るための暗号に応用されている」と言えるようになりましたね。
#数楽 双曲線で三角函数の加法公式を出す話をGeoGebraで。GeoGebra、初めて使ってみた。まだ使い方がよくわからん。https://www.geogebra.org/o/jffcf3fz
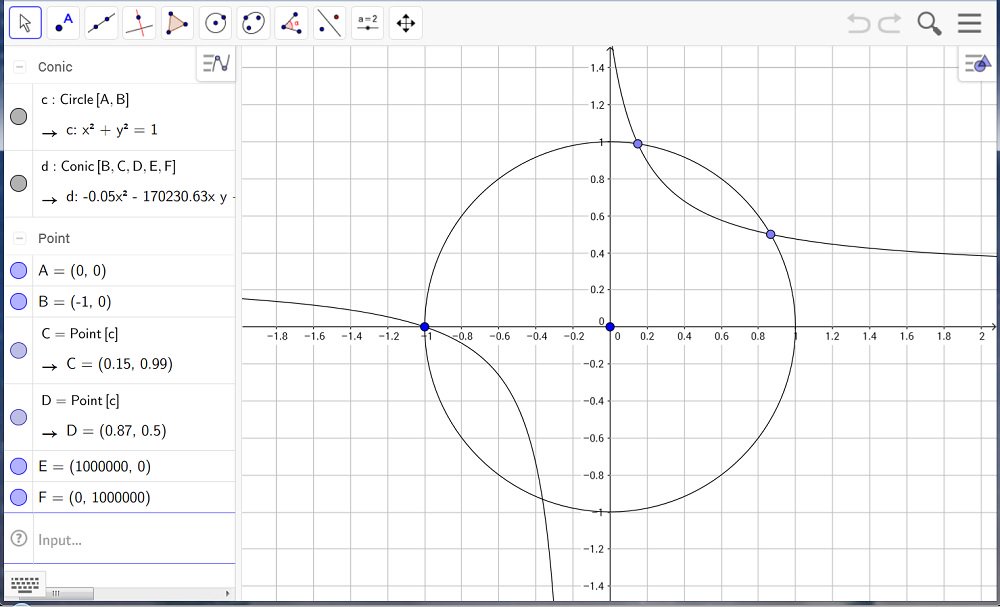
#数楽 https://www.geogebra.org/o/jffcf3fz はこんな感じ。円周上の2点を動かしてみて下さい。pic.twitter.com/wvIiVKTLxj

#数楽 GeoGebraで楕円曲線のEdwards form 0.03x^2+y^2=1+dx^2y^2のパラメーターdと点A,Bを動かせます。点Cは自動的に決まり、楕円曲線のAbel群構造でA+B+C=0が成立しています。https://www.geogebra.org/m/nFmHrqKW pic.twitter.com/UA3pq8xgIC
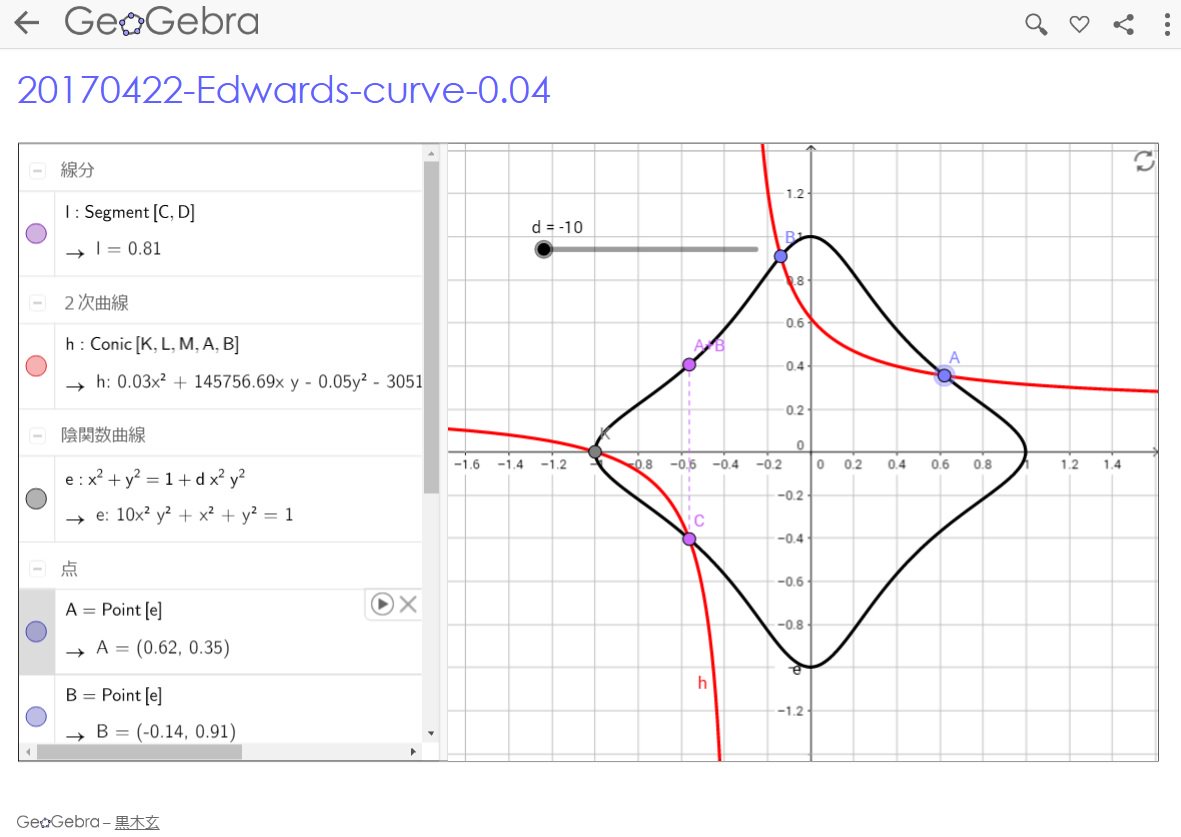
#数楽 GeoGebraで楕円曲線のEdwards form 0.04楕円曲線のAbel群構造についてA+B+C=0です。点D=A+Bと線分CDを追加しました。https://www.geogebra.org/m/hnvMuRtb pic.twitter.com/H6obDEubLZ
#数楽 体Kがdが平方根を含まないならば、Edwards曲線x^2+y^2=1+dx^2y^2は無限遠にK有理点を持たないので、有限のK有理点全体で閉じた群になります。例えば実数体上ならd≦0で実xy平面上のEdwards曲線は群になります。dを変化させるとその様子がわかります。
#数楽 Windows 7 64bit上のGeoGebraを使ってみたら頻繁にメニューが表示されなくなるというような不具合に遭遇したので結構困りました。現在はWin7機ではChrome上でGeoGebraを使っています。GeoGebraはまだ合計で数時間しか使っていない。
#数楽 GeoGebraでパラメーターのスライドバー付きの図やグラフを作ってpublicで公開しまくっておけば結構気軽に教育に役立つかも。プログラムを書くよりはずっと楽かも。publicに保存しておけば自分のウェブサイトを作る必要さえない。
#数楽 Edwards曲線に関する情報追加https://github.com/flyspeck/publications-of-thomas-hales/tree/master/cryptography/group_law_edwards …Mathematicaのコードなどが置いてある。楕円曲線関係でEdwards曲線について講義をすることになった人は参考にするべきかも。



